Google Summer of Code 2020 - Week 4
According to my GSoC proposal, I should be done with the general purpose graph layout capabilities for Rocs and free to start working on layout algorithms specifically designed to draw trees. This is not the case for a series of reasons, including my decision to write my own implementation of a general purpose force-based graph layout algorithm and failure to anticipate the need for non-functional tests to evaluate the quality of the layouts. I still need to document the functionalities of the plugin and improve the code documentation as well. Besides that, although it is not present in my original purpose, I really want to include the layout algorithm presented in [1], because I have high expectations about the quality of the layouts it can produce.
Even though I am not done with this first part, I decided to start working on the layout algorithms for trees. Now that I am more used to the code base and to the precesses used by KDE, I expect to be more productive and finish everything on time.
The main motivation for implementing layout algorithms specifically designed for trees is the possibility of exploiting the properties of trees to come up with better layouts. Yesterday, I started studying more about layout algorithms for trees. Most of them are based on a subset of the following ideas:
- Select a root node for the tree. This node can be provided by the user or selected automatically.
- Partition the nodes by their depth in the rooted tree and draw all nodes with the same depth at the same layer (usually a line or a circle).
- Draw the sub-trees in a recursive way and compose the resulting drawings to get the complete layout.
All of these ideas are related to the structure of trees. In order to improve my intuition about them, I wrote an experimental implementation based on the first two ideas above. The application of this implementation to a tree with 15 nodes generated the following result:
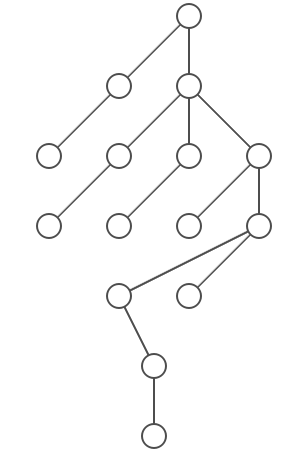
By taking advantage of the properties of trees, even simple solutions such as my one-day experimental implementation can guarantee some desirable layout properties that the general purpose force-based layout algorithm can not. For instance, it guarantees that there are no intersections between edges or between nodes. The force-based layout algorithm I implemented can generate layouts with pairs of edges that intersect even when applied to trees.
[1] R. Davidson and D. Harel. Drawing graphs nicely using simulated annealing.ACM Transactions on Graphics, 15(4):301–331, 1996.